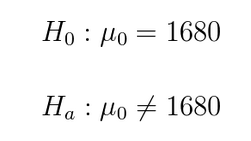Home › Topics › Learning Statistics › Critical Values and Hypothesis Testing

Critical Values and Hypothesis Testing

In statistical analyses, we usually need more than just the mean and standard deviation of a data set to make insightful conclusions. Additionally, we do not believe that the data is completely resilient to errors or noise. Additionally, we may believe that the sample mean is not the actual population mean. We believe this because it is distinctly possible that a large number of outliers were sampled and skewed the data. The two main introductory ways of doing this are confidence intervals and hypothesis testing. An important concept that we will need to understand confidence intervals and hypothesis tests is a critical value. Critical values basically state the final point in which we will accept values before changing our preconceived notions about the data. One of the main assumptions of these two tests is that the data came from a normally distributed population. Thus, we will go over the Shapiro- Wilk Test which tests for normality.

Critical Values

However, the use of z values does not stop at just comparing different observations from different populations as we did in the previous section. Usually we had a preconceived belief on the population of interest. For example, we may believe that a coin that we are flipping is fair. This means that heads and tails are equally likely. This would translate to a probability of .5 for each. We can use a statistical test to check if this hypothesis is correct. There are two ways of going about this. They are p values and critical values.

Critical values are the values at which we will have evidence to reject our hypothesis. These values are determined by the kind of question we are asking, but also the level of probability of being wrong we are willing to tolerate.   Let’s go over these 2 points individually and start with questions you are asking.

The critical values you need for statistical tests directly depends on the question you are asking (and also the type of test you will need to perform). The type of questions we will deal with will concern themselves with one tailed and two tailed hypothesis tests for normally distributed data. While we be going over the technical points on how to perform hypothesis tests in the next section, we wanted to informally introduce some of the topics first.

Depending on the question you are trying to answer, the probability you want to allow for being wrong could be different. Here is a simple example (try not to overthink it). If you were trying to predict who would win the World Series for fun, one could allow for more error. If you are wrong, there is no negative consequence. However, if you were trying to predict the same game, but instead of having fun, you were betting money on your prediction, then you would care a lot more if you were wrong. Thus for the second instance, you would desire a threshold that is smaller of being wrong.

Each critical value is associated with a probability. Many times, the probabilities chosen are .10, .05, and .01. If the data is more extreme then the critical value, we would favor a different hypothesis. Essentially, observing data with a smaller p value states that it very unlikely to observe the data you have, if your original hypothesis is correct.

We will go over how to find these values for each test as the approach is similar, but has one or two differences that matter. The two circumstances we will deal with are one tailed and two tailed tests. Before I begin, this next few paragraphs will be discussing one tailed and two tailed tests very informally. We wanted to discuss these in the manner so that we can talk about these tests in an informal manner to carefully wade into these tests. We want the analyst to be able to understand this test in an intuitive way as well as technical.

One tailed tests say that we would have evidence to reject our prior beliefs in only one extreme. For example, if we are playing a game with a friend by flipping a coin. Every time a head appears, your friend must give you $1. Every time a tail appears, you must give your friend $1. Before you play with your friend, you want to test if the coin is fair. However, you might only test if the coin is biased in the direction that puts you at a disadvantage. Thus, if we let p equal the probability of heads, you would find it permissible to find p to be .5 or greater. However, the alternative hypothesis is that p is less than .5. Thus, you would use the coin if the data suggested that p is fair or in your favor. Otherwise, you would use a different coin. Simply put, we would use the coin if each side appears equally or if we observe more heads. If we observe more tails than heads, we would have evidence that the initial guess is incorrect. To perform such a test, we would put the probability of rejecting and being wrong on one side. Figure 1 shows the values concerned for this critical value for a normal distribution. While the example does not relate to this distribution, we believe that the normal distribution is an easier to understand for beginners.

Figure 1
Figure 1

Two sided tests essentially state that we are concerned about data being too large or small in comparison to our original beliefs. Returning to our previous example, if we were concerned about being a good fair person, then we would want to confirm that the coin is not unbiased for heads or tails. Thus, we would be concerned if too many tails appeared, or if too many heads appeared. Figure 2 shows a two tailed test’s critical values and their rejection regions.

Figure 2
Figure 2

To better understand critical values and their usage, let’s formally discuss hypothesis testing.

Hypothesis Testing and Statistical Significance

An alternative way to test for inferences on data is by means of hypothesis testing. Hypothesis testing has a different approach. In life, we may believe that the parameter of interest has a true value. For example, we might believe that half of the population from the United States is Republican. However, over time, that proportion may change. We could believe that it has increased or decreased. Perhaps even, we believe that the proportion has changed, but we are not sure if it has increased or decreased. For example, if we believe that a heads occurs more often than tails, but not that heads occurs less than tails, then we will use a one sided test. However, if we are not sure if heads occurs more or less than tails, then we would use a two tailed test.

One-tailed Test

The setup for a one-tailed test would be as follows:

  H_0: p_0 \geq p

  H_a: p_0 < p

or

H_0: p_0 \leq p

  H_a: p_0 > p

p is the probability you believe it is. H_0 is the symbol used for the null hypothesis. This is what you believe about the population. H_a is the symbol used for the alternative hypothesis. The alternative hypothesis is what you are testing to see might be true. One tailed tests only check if the data is more extreme in one direction (ie higher or lower) but not both.

There are two ways to check if you have evidence to reject the null hypothesis. The first is after calculating the z value similar to out method in the previous section witch a slight change in the formula. The following is the way by which we will calculate a z score for a sample data set:

z =\frac{\bar{x}-\mu}{\sigma/\sqrt{n}}

Note that \bar{x} is the sample mean of the data set we will be observing. n is the symbol we use for the size of the data sample. If the z score is more extreme than the critical value, then we have evidence to reject the null. The second way is by calculating the p value of the z value that you calculated. p-values can be defined as the probability of observing a given value or more extreme. One can use a z table or R to find these p values. If the p value is less than the critical value’s p value, what we sometimes call \alpha, then we have evidence to reject the null. Interpreting this situation means that the probability of observing this data with the null hypothesis is very low. This means that it is very unlikely to occur, and thus, the data is more likely to occur from a distribution with a different parameter value.

Example 1

Assume that a beer company has scientifically created a scale that describes how good the created beer is. However, they find that there is variation between each batch. Their beer is normally distributed with mean 20 and standard deviation of 5. After some changes, the company wants to see if the alterations decreases the mean value and thus worse beer. The data can be found here. Perform a hypothesis test at an .10 significance level, or alpha.

Answer 1

The setup for this problem is as follows:

  H_0: \mu_0 \geq 20

  H_a: \mu_0 < 20

With a sample mean of 21.11262, the associated z score is calculated as follows:

z =\frac{\bar{x}-\mu}{\sigma/\sqrt{n}}

z =\frac{21.11262-20}{5\sqrt{10}}

z =\frac{1.11262}{1.581139}

z = .7037

The associated z critical value with this test is 1.645. Since the z score does not exceed the z critical value, we do not have evidence to reject the null. Additionally, since the associated p value of the z score is 0.7592 is greater than .10, we do not have evidence to reject the null. Thus, we have evidence that the population mean is 20.  Below is the code for this problem.

library('BSDA')

load('Beer Batch Sample.RData')

ls()

z.test(beer, mu=20, sigma.x=5, alternative="less", conf.level = 0.90)

As an aside, the data that I created this did not come from a distribution with mean 20 and standard deviation of 5. While it was still normal, it is possible that the test will not be able to always work. Something to keep in mind.

Two-tailed Test

The setup for a two-tailed test would be as follows:

  H_0: p_0 = p

  H_a: p_0 \neq p

Two-tailed test check if the data suggests that the actual parameter of interest is lower or higher at the same time. It is important to note that the test itself does not suggest if it is higher or lower. However, we can observe the data itself and state whether it would be higher or lower. Determining the whether or not we have evidence to reject the null is similar to one-tailed tests. The first way, by means of comparing the z value and the critical values, is exactly the same as before. p-values do have a slightly process if you are using a table. For calculating the p-value using the table, one would find it using the same table, but then also multiplying that value by 2. This is important to do, as you need to consider those values that are just as extreme as the value you observed on the other side of the distribution.

Example 2

Assume that the population of the total amount of minutes each individual per month spends on Facebook is normally distributed with mean of 1680 and standard deviation of 700. Your analytics division provides you with the following sample of the amount of minutes 10 users spent on Facebook on the previous month. Do we have evidence that the amount of time has changed?

Answer 2

The wording of the question suggests that we need to utilize a two tailed test. Thus, we have the following setup:

  H_0: \mu_0 = 1680

  H_a: \mu_0 \neq 1680

Since it was not specified, we will use a significance level of 0.05. With a sample mean of 1618.179. The z score was calculated using the following:

z =\frac{\bar{x}-\mu}{\sigma/\sqrt{n}}

Using the above formula, the z score was

z =\frac{\bar{x}-\mu}{\sigma/\sqrt{n}}

z =\frac{1618.179-1680}{700\sqrt{10}}

z =\frac{-61.821}{221.359}

z = -0.2793

This z value has an associate p value of 0.78. Thus, using p values, we do not have evidence to reject the null. Additionally, the z critical values were plus and minus 1.96. Since the critical value does not surpass the critical value, we do not have evidence to reject the null. Thus, we have evidence that the mean of the population is 1680 minutes. Below is the code we utilized to do this in R.

As an aside, we should note that it is actually impossible for the given problem to actually be normally distributed. It is impossible to have negative time on Facebook, but it is a requirement of the normal distribution to go from infinity to negative infinity. Just food for thought.

library('BSDA')

load('Facebook User Sample.RData')

ls()

z.test(fb, mu=1680, sigma.x=700)